International Journal of Social Sciences and Scientific Studies (2022)

Listes de contenus disponibles sur: Scholar

The Impact of Adopting Think-Pair-Share through Guided Inquiry Learning of Mental Mathematics

Journal homepage: ijssass.com/index.php/ijssass

THE IMPACT OF ADOPTING THINK-PAIR-SHARE THROUGH GUIDED INQUIRY LEARNING OF MENTAL MATHEMATICS☆

Ruby Thomasa*

a.University of Bahrain

Received 18 May 2022; Accepted 15 June 2022

Available online 15 July 2022

2787-0146

A R T I C L E I N F O

Keywords:

Inquiry-based learning approach

Mmathematical efficiency

Mental mathematics

Think-pair-share strategy

A B S T R A C T

This study explored the effectiveness of the think-pair-share (TPS) method combined with the inquiry-based learning (IBL) of mental mathematics to improve teacher trainees’ mathematical efficiency. School Mathematics teachers are expected to develop numeracy skills and confidence in their students. Inquiry-based teaching is an academic methodology that invites learners to explore educational contents by investigating, posing, and solving questions to create interest and class engagement. When working as a group, students first think individually and then share ideas with classmates, making learning more effective. The teacher candidates’ mathematical efficiency was compared between before and after such training at various stages. Findings concluded that as students applied mental strategies, they developed a better understanding of number relations and encouraged creativity and efficiency.

1. INTRODUCTION

LMental mathematics is not the procedural knowledge behind timetables and information; instead, it is real-world uses of number fluency, mathematics, also problem-solving abilities without using computational devices (Rubenstein, 2001). A vast majority of the students do not realize or value the importance of mental calculation skills to get accurate answers quickly instead of using calculators. She stated a strategy of introducing in-class practice using mental computations in various forms. After making mental mathematics an essential part of her class, Rubenstein (2001) students became more confident in their reasoning skills, approach problems in multiple ways, and liberated from calculator dependence. The traditional way of teaching mathematics leads to a situation where students may dislike the subject or find it intimidating. Using inquiry-based learning (IBL) and Think-Pair-Share (TPS) approaches can overcome this challenge. According to Ferguson (2010) this approach has a positive effect on the mathematics achievement of students. In IBL, teachers use questions to help students learn through individual thought and investigation. Convergent and divergent questions used in the classroom will help students construct fresh ideas and interpretations (Biggs & Tang, 2011).

School Mathematics teachers are expected to develop numeracy skills and confidence in students. I found that students are over-dependant on calculators, lacking mental calculation skills and conceptual understanding; leads to inefficacy to perform self-calculations. The reason is that they do not possess a proper number sense or a strong connection with this and mental mathematics, which is crucial in ensuring confidence in mathematics. Students learn and understand mathematical concepts in many different ways (Race, 2010). Two of the seven factors which lead to successful learning are ‘learning by doing’ and ‘making sense of things.’ My current practice covers the curriculum content only by mere lecture method, without much importance on developing mental mathematics skills. By improving my current teaching practice, students can become confident in doing mental calculations. This study is significant as it sheds light on future mathematics teachers’ training to mould effective and competent teachers. This study may also open paths to doing similar tasks at various teacher training and other relevant content areas.

Researchers suggest an inquiry-based approach to teaching mathematics, emphasizing the discussion of strategies, is very beneficial. Among the recent investigations on techniques to tackle this, I found IBL most suitable. As a student-centred approach, I was motivated to help students improve mental calculation skills by the dialogic approach that allows them to learn, get a deeper understanding and support various learning needs. This method is assumed to provide students with more authentic mathematics experiences and increase motivation and interest, which is essential in mathematics teachers’ moulding. To align with the government’s plan, I have decided to teach mental mathematics on whole number operations such as addition, subtraction, multiplication, and division using the IBL approach. During the first cycle, I observed that while most students enjoyed the IBL, some lacked confidence in sharing their ideas or opinions. Biggs, J. & Tang, C. (2011) states that a conceptual change happens when they work collaboratively and exchange ideas with others, peers, and teachers.

Moreover, such activities will shape, elaborate, and deepen their understanding. They also stated that creating a healthy classroom climate with formal and informal interactions has a strong effect on learning. Hence, I have decided to imbed the TPS strategy along with the IBL in the second cycle. The variation in the middle of Think-Pair-Share and other shared methods is that every learner is given a chance to think quietly and work in small groups (pairs).

In contrast with operating in larger sets, students working in pairs tend to have more listening and talking time, leading to more significant observations and communication abilities, helping students play a more active part in decision-making and developing study skills be lifelong learners (Biggs & Tang, 2011; Caroll, 2007). The mental mathematics strategies used were bridging, partitioning, sequencing, compensating, repeated addition, doubling & halving, factoring, and chunking. Teachers need to be flexible in first-hand approaches and ignite students’ passion and enthusiasm in learning mathematics. However, only 15-20 minutes in a lecture for a short period is not adequate for better training through inquiry. This can be considered to be a limitation of this study.

Methods

Research Questions

This research attempts to respond to the following questions:

1. To what extent did the IBL approach coupled with TPS during the implementation of the mental math strategies influence the teacher trainees’ mathematical efficiency?
2. What are the students’ perceptions of their learning experience while applying the IBL and TPS approaches?

Plan of Action

The participants are 61 teacher trainees of 2^nd year Bachelor of Education. They have finished their foundation year with mathematics before getting into Year 1. However, most of them were not confident in doing the mental calculation. The study was conducted in two cycles as described below:

• Cycle 1: In this cycle, the students were exposed to learning experiences of mental math techniques using a guided IBL approach, focused on leading beyond general curiosity into critical thinking and understanding by exploring mathematical prompts. This cycle aimed to replace my traditional teaching style with this approach to improve learning, mental calculation skills, and mathematical efficiency. The lessons were essentially based around investigative questioning such as “How many different and interesting ways can you make this number?”, “How can you solve 35 – 19?” and “How can you solve 435 + 99”? and so on. When the teacher plays a guiding role, it positively affects the students’ more in-depth learning.
• Cycle 2: The paradigm was shifted to the IBL environment; however, students were not active initially. As the training progressed, they started involving in the discussions and inquiry. Few of them were reluctant to participate as they lack confidence. This realization awoke the second change, incorporating the TPS strategy. In the second cycle, the IBL approach was continued with embedding a collaborative learning strategy, think-pair-share, that encourages students to exchange their ideas in learning and practicing mental math strategies to be more confident and efficient in necessary calculations.

Data Collection Tools

To measure the participants’ mathematical efficiency, three tools were used for data collection to ensure triangulation, facilitate the validation of data through cross verification from more than two sources, and test the reliability of obtained outcomes through a convergence of information. Quantitative and qualitative methods were used in this study to provide a profound understanding of the effect of the IBL approach on learning mental mathematics. The instruments used were:

• An observation checklist was used to measure their level of confidence, pace, accuracy, and engagement. The Reformed Teaching Observation Protocol (Sawada et al., 2000), combined with mathematical principles from the Principles and Standards for School Mathematics (NCTM, 2000), provided the information relevant to be observed during the training sessions. I have designed this to support my goal to follow the above aspects.
• Regular mental math tests were given out to measure their progress. Three trials were designed to fulfil the purpose, evaluating basic facts of mental mathematics. It consisted of number-only mental calculation problems, consistent with the training provided. It had 20 questions awarding 1 point for each correct answer with some slight variations on the values, in consequence guaranteeing a similar difficulty level for all the tests, conducted at various stages, as Ruder and Schafer (2002) concludes.
• Semi-structured interviews were also conducted to know students’ perceptions of their learning experiences in applying various mental math strategies using the IBL in the two cycles. Structured questions for the interview were developed to guide the discussion and to arrive at a conclusion.

Result and Discussion

Both quantitative and qualitative data were analysed, and the findings were consistent with the literature.

Analysis of the Mental Math Test Scores

Before starting the first cycle, the students were given a mental math test (Test 1) as a baseline to monitor their development. At the end of the four weeks, a similar test was conducted (Test 2) to assess their progress due to the guided inquiry approach. Test 3 was born after creating a collaborative learning environment by including the TPS strategy and the IBL approach. Even though the second test’s average score did not show a remarkable improvement, the particular intervention showed more significant improvement. Table 1 shows the mental maths test’s descriptive statistics at the beginning and the end of each cycle.

Table 1: Descriptive Statistics of the three mental math tests conducted at various stages

The statistics clearly show the tremendous improvement after the second cycle. The result is consistent with Crawford, D. B., & Snider, E (2000), and many other research findings found similar tremendous progress through IBL. TPS’s use helped create opportunities for the learners to converse effectively with their peers, which made the lesson more enjoyable.

Figure 1 shows the tests’ explicit comparison with the observed grand mean (12.03) and the students’ progress. Even though there is an improvement at the end of cycle 1, the test’s marginal standard at the end of process 2 is much above the observed grand mean. This suggests that both the teaching approaches increased the achievement, but a remarkable increase was noted after the second cycle.

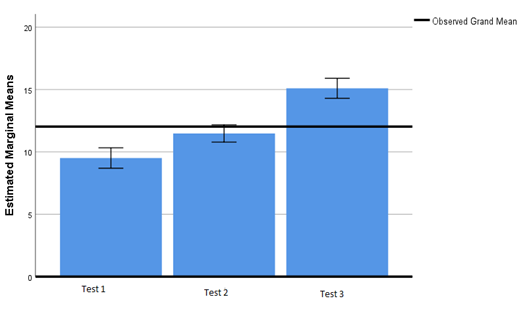
1. Figure 1: Mean scores of the three tests
2. The increased average test score may be an implication to the TPS embedded with the IBL.

Analysis of Lesson Observations

The teacher’s classroom management approaches, teaching style, and communications with learners at the classroom level can define how much is learned (Morrison, F. J., Bachman, H. J., & Connor, C. M., 2005). The observation checklist was assumed to measure specific inquiry details such as the confidence, pace, accuracy, and engagement of the students during the implementation. A further naturalistic observation was conducted multiple times by me and recorded the participants’ behaviour in the above areas. More focus was given on students’ engagement and confidence. The items were observed on a rating scale of 0-3. The diagram below provides a comparison of the data at the end of two cycles.

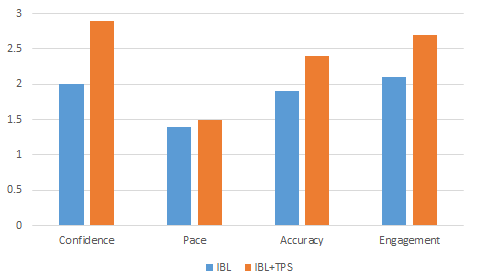
1. Figure 2: Analysis of classroom observations at the end of each cycle

As in figure 2, IBL proved that students were engaged and demonstrated confidence, and giving accurate answers at an average pace. However, with TPS’s incorporation, the engagement level increased, and they became very confident with more accurate answers. TPS will increase the number of students participating in whole-class discussion (Rowe, 1972). Even though they gained confidence, there is not much improvement in their pace. It needs extensive practice. Even though the IBL is meant to empower all the students, lack of confidence in the content matter deprived some of the active engagement. The amalgamation of the two (IBL+TPS) helped sort this issue to an extent, giving a large percentage of students engaged in learning and boosting their confidence. They demonstrated enthusiasm and mastery of content. Students will be actively engaged and continuously building self-confidence because it provides the students time to think (Lyman, 1987).

Analysis of Interviews

Interviews were conducted at the three stages (before starting the implementation of the IBL and at the end of each cycle) to comprehend the change in the perception about their learning experiences. Participants were interviewed, and the data were categorized into three themes: attitude, learning experience, and confidence. The analysis of the interviews showed that they liked this way of learning mental mathematics using the approaches. The interview codes and themes are pictorially represented in figure 3.

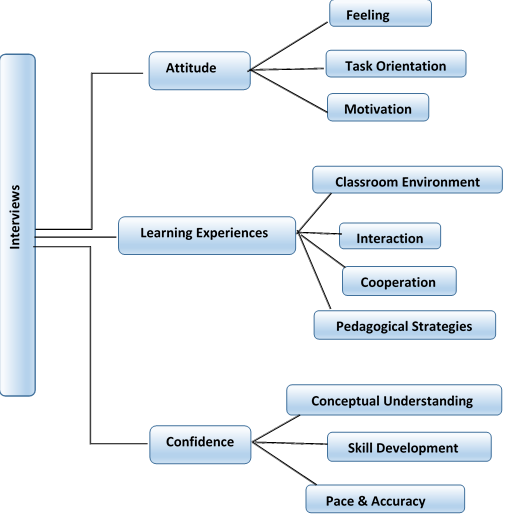
1. Figure 3: Interview Codes & Themes

Analysis of the theme: Attitude

Three codes, such as feelings, task orientation, and motivation, were used to measure the students’ attitudes. Some initial interview questions before the cycles showed apparent attitude change. Some of them commented that mental mathematics is complicated and it is not required as they have their mobile phones with them always. Their testimonies after the first cycle include: ‘at first, I feel that mental math is so hard, but now it is made easy’, ‘I enjoyed it as I am learning an important skill,’ ‘I found it as fun,’ ‘It motivated me,’ ‘this method helped me to be focused on my task’ and many more. After the second cycle, few more exciting responses came out, such as” it increased my motivation’, ‘this method motivated me,’ ‘making pairs and groups were beneficial,’ ‘I started using mental mathematics already’ and so on. However, one participant commented that she did not like mathematics from childhood, and still, she feels it as complicated. Here I am quoting Albert Einstein, “Genius is 1% talent and 99% percent hard work”, and he/she needs tremendous practice.

Analysis of the theme: Learning Experiences

The codes used to measure the learning environment’s effectiveness were classroom environment, interaction, pedagogical activities, and cooperation at the end of both cycles. They value the IBL as the best strategy and beneficial. Their testimonies revealed that the learning experience was thrilling and a different one as it enlightened their minds to think in various ways. They were very contented in getting time to think and give their answers. Some of their responses were ‘this approach improved my mental skills,’ ‘it was a different learning experience,’ and ‘I learned many ways to solve problems.’ Few participants openly said that they were afraid to give their answers because they were unsure about it, which shows a lack of confidence and conceptual understanding. At the end of the second cycle, the responses were more exciting as they were given time to think individually, discuss in pairs and then share with their classmates. As I walked around during the discussion time, I could feel that some students were very confident in sharing their process with their classmates. The socio-cultural theory by Vygotsky (1987) also states that classroom interaction increases the learning opportunities by cooperation.

Analysis of the theme: Confidence

Three codes were used to check students’ confidence level because of these learning experiences: conceptual understanding, skill development, pace, and accuracy in mental math calculation, which boost efficiency and confidence. The participants testified that the techniques explained using the IBL helped them solve the problems easily and quickly and improve their mathematical skills, gaining confidence. Gaining a conceptual understanding of numbers and their groupings using challenging inquiries made calculations more manageable. A few of their responses were ‘I improved on my calculation skills.’ ‘it changed my conceptual understanding about number grouping,’ ‘It helped me to think deeper,’ and ‘I have started doing questions without using the calculator.’ After the TPS strategy was embedded with the IBL, the students became more confident and improved their communication skills. Many of them agreed that this improved their mathematical skills and communication skills, hence, gaining conceptual understanding. Some of them affirmed that ‘I gained more knowledge,’ ‘this method increased my motivation in learning mental math,’ ‘this method let me think more and deep,’ ‘I can do calculations faster now,’ ‘It helped me to think faster and deep.’ The think-pair-share plays a vital role in developing students’ intellectual also cognitive skills (Lyman, 1987).

Conclusion

From the observed pieces of evidence obtained from quantitative and qualitative data analysis methods, it was evident that the IBL approach coupled with TPS in learning mental mathematics resulted in improved student mathematical efficiency and confidence. I am now convinced that these activities should not be restricted to mental mathematics alone but should be used in other topics. Even though the results are very positive, few students expressed their nervousness about the subject from childhood. With good practice, they can become confident and eliminate the limitation of this study.

This study helped me in my professional development in many ways. I agree with Ferguson (2010) that the implementation of IBL methods is an effort to improve education. The finding of this action research inspired me to shift my current practice to the student-centred paradigm.

Primarily, the student interviews and observations indicate that the improvement results from the increased interaction with students during the lesson, making it enjoyable. Hence, necessary opportunities should be provided for students to grow as critical thinkers. Secondly, student-engagement hindrances were removed while discussing with peers in a comfortable learning environment (Lyman, 1987). This promoted their self-efficiency, participation, conceptual understanding, and enjoyment in learning. Hence, I will include challenging but enjoyable collaborative activities while providing chances for learners to express their concepts and discussions. Thirdly, think-pair-share is amongst the cooperative learning methods which actively engage learners (Bell, 1998). I learned that it is my responsibility to foster a sense of independence and confidence. In IBL, the teacher acts as the facilitator of the students’ learning rather than the information provider (Crombie, I. K & Davis, H.T 2009). I intend to put this into practice using open-ended questions.

References

Bell, J. (1998). Improving Student Learning and College Teaching. Ideas on Lecturing from a Variety of Places and People, Ideas on Cooperative Learning and the Use of Small Groups. Howard Community College.

Biggs, J., & Tang, C. (2011). Teaching for Quality Learning at University. Maidenhead, UK: Open University Press.

Brune, M.C. (2010). The Inquiry Learning Model as an Approach to Mathematics Instruction. Unpublished Master Thesis. Boise, ID: Boise State University.

Carroll, K. (2007). A Guide to Great Field Trips. Chicago: Chicago Review Press.

Cockcroft, W.H. (1982). Mathematics counts. Report of the Committee on Inquiry into the Teaching of Mathematics in Schools. HMSO, London.

Crawford, D. B., & Snider, E. (2000). Effective mathematics instruction: the importance of curriculum. Education and Treatment of Children.

Crombie, I .K & Davis, H.T. (2009). What is a Meta-analysis? London: Hayward Medical Communications.

Echevarria, J., Vogt, M. E., & Short, D. (2004). Making content comprehensible for English learners: The SIOP model (2^nd ed.). Boston: Pearson Allyn & Bacon.

Ferguson, K. (2010). Inquiry Based Mathematics Instruction Vs Traditional Mathematics Instruction: The Effect on Student Understanding and Comprehension in an Eighth Grade Pre-Algebra Classroom. Cedarville: Cedarville University.

Lyman, F. (1987). Think-Pair-Share: An Ending Teaching Technique. MAA-CIE Cooperative News, 1, 1-2.

Mcintosh, A. J. (1990). Becoming numerate: developing number sense. Hawthorn: ACER.

McTighe, J., & Lyman, F.T. (1988). Cueing thinking in the classroom: The promise of theory embedded tools. Educational Leadership, 45(7)., 18-24.

Morrison, F. J., Bachman, H. J., & Connor, C. M. (2005). Improving literacy in America: Guidelines from research. New Haven, CT: Yale University Press.

National Research Council (2000). Inquiry and the national science education standards: A guide for teaching and learning. Washington, DC: National Academy Press.

NCTM: National Council for Teachers of Mathemtics (2000). Principles and Standards for School Mathematics. Reston, VA: NCTM

Race, P. (2010). Making Learning Happen: A guide for post-Compulsory education (2nd ed.). London, SAGE Publications Ltd.

Rowe, M. (1972). Wait-time and rewards as instructional variables: Their influence on language, logic, and fate control: Part II, rewards. Journal of Research in Science Teaching,11 (4), 291-308.

Rubenstein, R. (2001). Mental mathematics beyond the middle school: Why? What? How? Mathematics Teacher. 94(6)., 442-446.

Rudner, L. and W. Schafer (2002). What Teachers Need to Know About Assessment? Washington, DC: National Education Association.

Santrock, J.W. (2001). Educational Psychology. United States of America: McGraw-Hill Companies, Inc.

Sawada, D., Piburn, M., Falconer, K., Turley, J., Benford, R., & Bloom, I. (2000). Reformed Teaching Observation Protocol (RTOP). (ACEPT Technical Report No. IN00-1). Tempe, AZ: Arizona Collaborative for Excellence in the Preparation of Teachers.

Stevens, R. J., & Slavin, R. E. (1995). Effects of a cooperative learning approach in reading and writing on academically handicapped and non-handicapped students. Elementary School Journal, 95, 241–262.

Vygotsky, L. S. (1987). The collected works of L. S. Vygotsky: Vol. 1. Problems of general psychology (R. W. Rieber & A. S. Carton, Eds.).. New York, NY: Plenum.

☆ The Impact of Adopting Think-Pair-Share through Guided Inquiry Learning of Mental Mathematics

* Corresponding author at: .Ruby Thomas, University of Bahrain

Received 18 May 2022; Accepted 15 June 2022

Available online 15 June 2022

2787-0146