ABSTRACT
Introduction : Le comportement humain est un élément clé de la transmission et la persistance de l’épidémie ebola. Nous présentons ici les modèles épidémiologiques de sa transmission.
Méthodes : Modèles non déterministes utilisés. Les dérivées d/dt nous ont donné la variation des fonctions du modèle en fonction du temps t, afin d’en décrire l’évolution pendant la durée de l’épidémie.
Résultats : Le théorème de Bayes est bien applicable dans la modélisation de ebola et à l’absence des mesures strictes, la probabilité P(M) pour qu’un cas confirmé génère un autre est de 100%. La moyenne µ pour les cas attendus selon le modèle appliqué a été de 3072 cas et le nombre des cas observés (3470) est légèrement supérieur à cette moyenne (courbe de Gauss). Le nombre des malades était multiplié par 2 tous les 50 jours et l’épidémie.
Conclusion : La mise en place d’équations pour décrire l’épidémie de façon reproductible et simulable donne une idée sur l’évolution de la maladie
INRODUCTION
Depuis la découverte du virus Ebola, 15 épidémies ont été enregistrées en République Démocratique du Congo depuis sa première éclosion en 1976.
La maladie a sévi en Afrique équatoriale, les épidémies se succédant de 1976 à 2014 dans cinq pays : la RDC, le Soudan, le Gabon, l’Ouganda et le Congo. Plus de 2 000 cas ont été rapportés avec plus de 1 500 décès. La MVE était donc relativement limitée au point de vue géographique jusqu’à l’épidémie apparue en Afrique de l’Ouest fin 2013 [1].
La République démocratique du Congo (RDC) est confrontée à de multiples situations
d’urgences de santé publique, notamment aux épidémies de maladies infectieuses telles que la Maladie à virus Ebola (MVE). Le pays s’illustre en effet par l’émergence et des résurgences successives d’épidémies de MVE. Il a ainsi été confronté, il y a seulement environ une année, à une 12e épidémie de MVE. Ces flambées épidémiques qui constituent une menace pour la sécurité sanitaire nationale et internationale sont à l’interface entre la santé humaine, animale et environnementale. Au sortir des 9e, 10e, 11e et 12e épidémies de MVE, d’autres épidémies (rougeole, polio, choléra, fièvre jaune, anthrax, peste, etc.) et de catastrophes naturelles ; l’analyse diagnostique et prospective de la riposte aux 4 dernières épidémies de MVE montrent la nécessité de renforcer la coordination et les capacités des acteurs de la riposte tant du niveau central que périphérique [2].
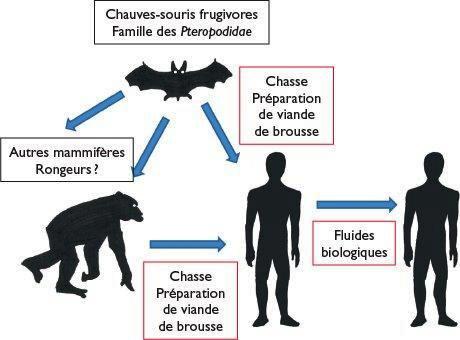
Figure 1 : Réservoir et hôtes du virus
Une des stratégies capitales dans la gestion de la chaine de transmission est la recherche des contacts. La recherche des contacts est un processus qui consiste à identifier, évaluer et suivre les personnes qui ont été exposées à la maladie pour éviter que l’infection se propage. Les sujets susceptibles d’avoir été exposés à Ebola sont systématiquement mis en observation pendant 21 jours (période maximale d’incubation de la maladie) à compter de la date de l’exposition la plus récente. Cette démarche permet une identification rapide des personnes qui deviennent symptomatiques. En identifiant les malades dès l’apparition des symptômes et en les isolant rapidement, on réduit le risque que d’autres personnes soient exposées, évitant ainsi de nouvelles infections. En outre, lorsqu’un patient symptomatique est isolé et admis rapidement dans un centre de soins, son traitement peut démarrer plus tôt, augmentant ses chances de survie [3]. Une recherche des contacts bien menée combinée à un bon isolement est une meilleure stratégie que chacune de ces mesures prises séparément. Pour l’isolement nous proposons le centre de transit comme solution durable (vu la conception socio anthropologique des épidémies dans la région et la peur de mourir au CTE). Il est connu que les cas contacts ainsi que les suspects ont une gestion particulière qui permet de couper la chaine de transmission. Pour chercher à comprendre ce qui se passe, ne pas se contenter d’une solution empirique, il est important de décrire de manière scientifique, quantitative (par exemple en termes d’équations), une épidémie de la maladie à virus ebola. La modélisation mathématique des maladies infectieuses est un outil pour : étudier la façon dont les maladies se propagent, prévoir la trajectoire future d’une éclosion, aider à orienter la planification de la santé publique et la lutte contre les maladies infectieuses. En RDC, une étude a montré que les personnels de santé avaient une connaissance insuffisante sur le suivi des contacts de la MVE et cela implique un sérieux problème dans la gestion de la chaine de transmission [4].
En plus des mouvements de population, l’une des difficultés récurrentes pour l’intervention est la peur de la communauté envers cette maladie très meurtrière, qui peut rendre difficile la relation avec les acteurs de la riposte. Cela se traduit par une certaine réticence à lancer l’alerte sur les cas suspects, se rendre aux centres de traitement et accepter l’accompagnement des équipes qui assurent les enterrements dignes et sécurisés. Il avait été constaté un besoin d’une communication meilleure et plus efficace de la part de tous les acteurs de la riposte afin de gagner la confiance de la population. Certes, la mortalité de la maladie est très élevée. La solution était d’intégrer les soins aux suspects et contacts d’ebola dans les hôpitaux, rester ainsi proche des structures où la population est traitée d’ordinaire.
Dans la surveillance des d’épidémies comme la maladie à virus Ebola qui présente un taux mortalité extrêmement élevé, il est important de disposer d’outils numériques, que ce soit pour le suivi en temps réel des besoins potentiels immédiats en termes d’infrastructure d’urgence, bref d’un riposte de qualité très élevée.
Lors de la pandémie Covid 19, les modélisations mathématiques ont connu un essor lors de la prise de décision relatives aux politiques de santé publique et a également contribué à l’épidémiosurveillance de la maladie
Une grande majorité des modèles de maladies infectieuses s’appuie sur des modèles compartimentaux dans lesquels la population est virtuellement divisée en un nombre de compartiments donnés qui interagissent entre eux selon certaines règles [5]
Modéliser la dynamique d’une épidémie comme Ebola s’avère toutefois particulièrement délicat en raison de la variabilité observée d’une épidémie à l’autre, tout particulièrement lors d’une épidémie d’une grande ampleur comme la 10è épidémie observée dans les provinces du Nord-Kivu et de l’Ituri en RDC
Notre étude avait comme objectif général d’expliquer mathématiquement la dynamique de transmission de la maladie à virus ebola et permettre aux décideurs politiques de mettre en place et en temps des stratégies de riposte et une veille sanitaire permanente.
Objectifs spécifiques :
- Représenter la chaine de transmission de la MVE en fonction de la loi normale
- Déterminer la période durant laquelle le nombre des cas confirmés peut doubler durant l’épidémie.
- Déterminer les probabilités pour les différents compartiments de la chaine de transmission de la MVE selon le théorème de Bayes
METHODOLOGIE
Milieu d’étude
Les deux provinces du Nord-Kivu et de l’Ituri ont connu la dixième épidémie de la maladie à virus ebola qui était très meurtrière. Les deux provinces abritent environ 10 millions d’habitants qui vivent en majorité de l’agriculture et du commerce [ ]. Les mesures de surveillance épidémiologiques y sont insuffisantes et les provinces restent en état d’alerte vis-à-vis d’éventuelles épidémies. La population locale développe vite des rumeurs devant tout événement étrange comme une épidémie de fière hémorragique et devient réticente aux équipes de ripostes.
![PDF] Epidémiologie et contrôle de la theilériose bovine à Theileria parva dans la Province du Nord-Kivu, République Démocratique du Congo | Semantic Scholar](https://ijssass.com/journal/wp-content/uploads/2024/10/pdf-epidemiologie-et-controle-de-la-theileriose-b.png)
Fig. 2. Carte géographique montrant les zones touchées par la 10è épidémie de la MVE
Type d’étude :
Nous avons réalisé une étude descriptive portant sur les données de toute la période de la 10è épidémie de la MVE.
Hypothèses des modèles
- Les individus sains exposés au même niveau sortent différemment du risque pour développer la maladie :
- L’augmentation des cas confirmés est fonction du nombre des contacts dans la communauté
- Le passage dans un centre de transit ralentit le risque de contamination dans la communauté. A l’absence du CTE, tout cas confirmé a 100% de risque de générer un autre dans la communauté.
- L’évolution de l’épidémie de la maladie à virus ebola suit la Loi normale.
Variables des modèles
- Individus sains S(t) : sans aucun symptômes et qui vit dans la communauté soit dans un ensemble (R)
- Les contacts C(t): personne n’ayant pas de symptômes mais qui a été en contact physique avec un cas probable ou confirmé ou avec ses liquides physiologiques au cours des 21 jours précédents (par exemple soins d’un malade, participation à un rite funéraire, manipulation d’échantillons de laboratoire potentiellement contaminés).
- Les malades M(t) : Tout cas probable ou suspect confirmé par le laboratoire
- Guéris G(t) : des anciens cas positifs devenus négatifs après une prise en charge.
Dans notre modèle, α va représenter le taux de d’exposition entre S(t) et C(t) soit la population saine et les contacts, β va représenter le taux de confirmation (ou de transmission) entre C(t) et M(t) soit entre les contacts et les malades, et γ le taux de guérison entre M(t) et G(t). Nous pouvons ainsi noter :
α β γ
S C M G
Méthode
La population sera scindée en 3 groupes : les sains, les confirmés et les guéris (SCMG). Ceci en comparaison avec le modèle SIR (sains, infectés et retirés) présenté dans certaines modélisations épidémiologiques [6]. Nous allons considérer R0 comme nombre de reproduction initial soit le nombre moyen d’individus contaminés par une personne, lorsque cette personne infectée apparaît dans une population uniquement composée d’individus susceptibles d’être contaminés. R0 va de 1,5 à 2 pour la maladie à virus ebola [7].
Etant donné que C sont des contacts, M le cas confirmés et G les guéris, D les décédés, nous pouvons noter les différentes probabilités de notre modèle sachant que C et M sont deux événements indépendants :
P(M) est la probabilité de devenir cas confirmé, P(C), la probabilité d’être contacts. P(C/M) est la probabilité que les contacts aient existé quand on a les cas et P(M/C) est la probabilité que les cas confirmés existent étant donné que les contacts soient enregistrés.
Ainsi : , c’est l’application du théorème de Bayes pour notre modèle.
RESULTATS / CONSTRUTIONS DES MODELES
Dans ce modèle, nous allons étudier la taille de ces trois sous-populations au cours du temps t. Et donc S(t) représente les personnes saines au temps t, C(t) les contacts non encore contagieux au temps t, M(t) les malades ou cas confirmés au temps t, et G(t) les personnes guéries qui sont donc immunisées. Ainsi N=S(t)+C(t)+M(t)+G(t) représente alors la population constante totale de toute la ville au cours du temps. Les cas contacts ou exposés, qui ne sont donc pas contagieux, sont représentés par la fonction C(t) ; ce qui permet de prendre en compte la durée d’incubation (via β) d’une maladie.
La succession mathématique des modèles est la suivante :
– γM(t)
γM(t)
Comme S(t) doit subir des modifications suites aux naissances, nous allons ajouter un terme vN(t), on aura S(t)+ vN(t) et écrire
+vN(t) considérée donc comme population saine car les nouveau-nés viennent au monde sans virus.
Par ailleurs, comme il peut y avoir des personnes qui meurent quelque soit leur état SCMG de cause non liée à la MVE, nous allons soustraire de chaque composante le taux de décès soit µ. Les équations deviendront :
+vN(t)-µS(t)
-µC(t)
– γM(t)-µM(t)
γM(t)-G(t)
Les dérivées d/dt permettent de connaître la variation (c’est à dire si c’est croissant ou décroissant) des fonctions S,C,M,G en fonction du temps t, afin d’en décrire l’évolution au cours du temps. La dérivée d’une fonction d’une variable réelle mesure l’ampleur du changement de la valeur de la fonction (valeur de sortie) par rapport à un petit changement de son argument (valeur d’entrée). Lorsqu’une grandeur est fonction du temps, la dérivée de cette grandeur donne la vitesse instantanée de variation de cette grandeur, et la dérivée de la dérivée donne l’accélération.
Soit f une fonction définie sur un intervalle I. On dit que f est dérivable sur I si elle est dérivable en tout réel x de I. Dans ce cas, la fonction qui à tout réel x de I associe le nombre dérivé de f en x est appelée fonction dérivée de f et se note f ‘. Considérées comme des fonctions, les S,C,M,G vont subir des changement sur et la distance entre S et G comme l’intervalle.
Pour la maladie à virus ebola, R0 va de 1,5 à 2 [6]. Ainsi 1C=2M et M=0,66D+0,34G au temps 1. Donc le nombre des malades dépendra des nombres des contacts, le nombre des décès et des guéris dépendra du nombre des malades. Dans notre milieu d’étude, La maladie avait fait 250000 contacts selon l’OMS, 3470 cas confirmés dont 2287 décès soit 66% de létalité et 1171 survivants [8]. Nous voulons aussi connaitre mathématiquement, combien des personnes étaient des vrais contacts susceptibles de présenter la maladie.
Sachant que R0 est le nombre de reproduction initial soit le nombre moyen d’individus contaminés par une personne, lorsque cette personne infectée apparaît dans une population uniquement composée d’individus susceptibles d’être contaminés. R0 va de 1,5 à 2 pour la maladie à virus ebola [7]. Le temps t représente la vague de contamination. Avec l’échantillon de n contacts, on en déduit le tableau qui suit :
Tableau n° I. Présentation mathématique de l’évolution de l’épidémie à partir des contacts
| Temps | Contacts | Malades | Guéris | Décédés |
| 0 | 250000 | 1 | 0 | 0 |
| 1 | 249998 | 2 | 0,34 | 0,66 |
| 2 | 249294 | 4 | 1,02 | 1,98 |
| 3 | 249286 | 8 | 2,38 | 4,62 |
| 4 | 249270 | 16 | 5,1 | 9,9 |
| 5 | 249238 | 32 | 10,54 | 20,46 |
| 6 | 249174 | 64 | 21,42 | 41,58 |
| 7 | 249046 | 128 | 43,18 | 83,82 |
| 8 | 248790 | 256 | 86,7 | 168,3 |
| 9 | 248278 | 512 | 174,08 | 337,92 |
| 10 | 247254 | 1024 | 347,82 | 675,18 |
| 11 | 245206 | 2048 | 696,32 | 1351,68 |
| 12 | 241110 | 4096 | 1392,64 | 2703,36 |
Durant la 10è épidémie, 3469 contacts soit 1,4% de avaient développé la maladie. Le reste soit 98,6% ne l’ont pas fait. Les facteurs de protection ont été, entre autres, le vaccin reçu par plus de 303 000 personnes dans la région affectée. Dans le tableau ci-dessus, le nombre des cas confirmés durant l’épidémie se retrouve entre le T11 et le T12 soit entre 2048 et 4096. La moyenne µ est de 3072 cas et le nombre des cas observés (3470) est légèrement supérieur à cette moyenne. Nous pouvons ainsi représenter ca dans un intervalle de 2,048 à 4,096 : [2, 4] et tracer la courbe de Gauss. La loi normale centrée réduite est la loi de probabilité absolument continue dont la densité de probabilité est donnée par la fonction ![]() φ : R → R + définie par [8]
φ : R → R + définie par [8]
2
3
4
3,47
0,97
1,94
![]() pour tout t apprenant à R. La variable aléatoire X qui suit la loi normale centrée réduite est notée
pour tout t apprenant à R. La variable aléatoire X qui suit la loi normale centrée réduite est notée
![]()
Les malades
Les décédés
Les guéris
Dans notre modèle α β γ
S C M G
β est quasiment considéré comme le vaccin.
Modèle selon le théorème de Bayes
Considérant les probabilités pour les différents compartiments :
, c’est l’application du théorème de Bayes pour notre modèle. Les courbes qui en ressortent :
Si le vaccin demeure la seul mesure pour qu’un contact ne soit pas malade, alors à l’absence du vaccin P(M) devient 1 soit 100%. L’équation devient . Or P(C) dépend étroitement, elle, des mesures mises préventives en places par les équipes de ripostes. Ainsi en cas d’absence des mesures P(C) va tendre vers 1 entrainant une P(M/C) approximativement égale à P(C/M).
Dans cette modélisation nous pouvons montrer que la probabilité qu’un cas confirmé génère un autre à l’absence d’un centre de traitement Ebola (CTE) est de 1 soit 100% en revenant au théorème de Bayes :
Or P(M/C) = P(M∩C)/P(C) et P(C/M)=P(C∩M)/P(M)
L’équation devient alors :
P(M∩C)/P(C) = , comme schématiquement dans la logique de la MVE, à l’intersection de l’ensemble des contacts et des malades on ne peut qu’avoir des malades
MALADES
M
C
CONTACTS
P(M)/P(C)=
P(M)=1
DISCUSSION
Notre étude est partie d’une probabilité pour un cas confirmé à générer deux autres et le territoire d’étude prenait une étendue de 4500Km2 comparativement aux deux pays le Liberia et la Sierra-Leone. Les cas rapportés au Liberia doublent tous les 15–20 jours, et ceux en Sierra Leone doublent tous les 30–40 jours. Dans notre milieu d’étude l’épidémie avait duré 660 jours (618 jours avec des cas confirmés) et avait fait 3470 malades soit 5 à 6 par jour. Considérant le tableau généré par notre modèle, nous trouvons que le nombre des malades doublait plutôt tous les 51 à 52 jours. S’appuyant sur le succès de l’endiguement de la 9e maladie à virus Ebola dans la région de l’Équateur (déclarée terminée après seulement trois mois le 24 juillet 2018), le gouvernement s’est lancé dans « la réponse la plus rapide, la mieux équipée et la mieux
financée de l’histoire de la riposte à l’épidémie d’Ebola » pour faire face à la 10e maladie à virus Ebola [9]. Un plan de réponse stratégique (SRP1), couvrant la période août-octobre 2018, avait défini le modèle de réponse, avec une coordination structurée comme dans les réponses antérieures, autour de huit piliers d’action : surveillance (y compris recherche des contacts, points d’entrée et vaccination), laboratoires, gestion des cas, communication des risques et engagement communautaire (RCCE), soutien psychosocial, prévention et contrôle des infections (y compris des enterrements sûrs et dignes), logistique et sécurité.
Peu de temps après la déclaration de l’épidémie, le Ministère de la Santé a commencé à administrer un vaccin expérimental (le rVSV-ZEBOV de Merck, sans licence mais qui s’est avéré protecteur dans les essais aux derniers stades de l’épidémie en Afrique de l’Ouest)
Beaucoup d’efforts devront être faite sur la transmission de la MVE dans une population dense en mouvement des affaires sur l’axe Goma-Butembo-Beni-Bunia-Mambasa. L’outil de modélisation EbolaResponse avait également été utilisé pour estimer comment les interventions de contrôle et de prévention pourraient ralentir et finir par mettre un terme à l’épidémie. Notre étude a été axée sur la chaine de transmission de la maladie à virus ebola jusqu’aux modalités de sortis pour les cas confirmés. L’outil de modélisation appelé EbolaResponse utilisé par CDC en Afrique de l’Ouest était destiné à une estimation des nombres possibles de cas futurs. Dans ce model Il a été également calculé un facteur de correction des erreurs de sous-estimation possible du nombre de cas rapportés, établi à 2,5 [11]
Dans une étude sur un modèle d’Ebola avec incidence proportionnelle, les auteurs avaient évalué grâce à l’analyse de la sensibilité l’importance des stratégies de contrôle telles que la mise en quarantaine et la vaccination. Ils ont montré que, la mise en quarantaine, implémentée par la recherche des contacts et l’isolement sont des stratégies de contrôle très efficaces pour réduire le degré de la maladie, mais les combiner à la vaccination déboucherait à une élimination de la maladie à virus Ebola [12].
L’application du théorème de Bayes montre bien qu’à la absence des CTE, tout cas confirmé génère un autre et donc difficile de circonscrire et en finir avec une épidémie. Le rôle de la communauté devient capital dans la gestion de la MVE. Les collectivités touchées par une épidémie d’Ebola ont notamment besoin d’aide pour accéder aux services essentiels à la vie et aux moyens d’existence. Une épidémie d’Ebola ne peut être maîtrisée avec succès que si les populations touchées sont en mesure de se l’approprier, de prendre les mesures qui s’imposent et de modifier leur façon de vivre afin de réduire son emprise sur leurs sociétés. Elles changent leur comportement de façon à réduire le risque de transmission de l’Ebola au sein de leur collectivité, notamment en identifiant et en signalant rapidement les personnes atteintes de la maladie, en s’isolant elles-mêmes et en modifiant leurs pratiques curatives et leurs rites d’inhumation traditionnels.
Conclusion
La modélisation mathématique permet d’expliquer des phénomènes complexes dans lesquels interviennent des processus divers. Elle est aujourd’hui l’un des domaines les plus prisés de la science.
Nous avons montré, d’après nos estimations, que quand R0 est de 2, on déduit que, si des mesures de contrôle ne sont pas implémentées, la maladie va se propager. Nous avons exploré par ailleurs l’effet de la mobilité des populations sur la propagation de la maladie en considérant le modèle en fonction du temps t considéré comme la vague de contamination avec des paramètres égaux dans tous les compartiments(sains, contacts, cas confirmés , guéris et décès). Ce qui biologiquement signifie que, lorsque le nombre de reproduction contrôlé est inférieur à 1, la maladie va disparaitre assez rapidement, alors que s’il est supérieur à 1, elle peut persister.
Le travail a proposé un modèle épidémique avec dépistage à l’entrée et à la sortie des compartiments : les infectés dépistés positifs sortent aux frontières de leur compartiment sous différentes modalités. Les simulations numériques nous montrent qu’une recherche parfaite des contacts est meilleure qu’un isolement parfait, qui lui est meilleure qu’une mauvaise recherche des contacts, mais qu’une bonne combinaison de ces deux stratégies de contrôle est meilleure que chacune d’entre elle prise séparément et implémentée avec perfection. Le passage dans un centre de transit ralentit le risque de contamination dans la communauté, il doit être intégré dans les structures de soins lors d’une épidémie de la MVE.
Remerciement : Nous disons merci aux autorités des zones de santé touchées par cette épidémie pour avoir collaboré dans l’obtention des données de cette étude.
REFERENCES
- Docteur Bernard-Alex Gaüzère, Professeur Pierre Aubry, Maladie à virus Ebola. Actualités 2021. Centre René Labusquière, Institut de Médecine Tropicale, Université de Bordeaux, 33076 Bordeaux (France).
- Ministère de la santé publique. Rapport technique : revue après action de la riposte aux 9e, 10e, 11e et 12e épidémies de maladie à virus Ebola en République démocratique du Congo, OMS Juin 2021.
- OMS. Mise en œuvre et gestion de la recherche des contacts pour la maladie à virus Ebola, consulté le 10 mai 2023.
- Augustin Mapendo Ndaliko, and Jean-Bosco Kahindo Mbeva. “Knowledge, attitudes, and behaviors of healthcare professionals at the start of an Ebola virus epidemic.” Infectious Diseases Now 51.1 (2021): 50-54.
- Julie Mintsa mi ondo Mintsa Mi Ondo. Spatial aspect in the epidemiological modeling. Theses, Université de Grenoble, November 2012.
- OUEMBA TASSE ARSENE JAURES, Modélisation mathématique de la transmission de la maladie à virus Ebola et stratégies de contrôle , thèse de doctorat , mai 2021
- Althaus CL. Estimating the Reproduction Number of Ebola Virus (EBOV) During the 2014 Outbreak in West Africa. PLoS Curr. 2014 Sep 2;6:ecurrents.outbreaks.91afb5e0f279e7f29e7056095255b288.doi: 10.1371/currents.outbreaks.91afb5e0f279e7f29e7056095255b288. PMID: 25642364; PMCID: PMC4169395.
- Sepp Hochreiter, Djork-Arne Clevert et Klaus Obermayer, « A new summarization method for affymetrix probe level data », Bioinformatics, vol. 22, no 8, 2006, p. 943-949 (DOI 10.1093/bioinformatics/btl033).
- IOAC – Comité consultatif et de supervision indépendant pour le programme de l’OMS pour les urgences sanitaires (2019a) Du « plus jamais » à « nouvelle normalité » : que nous apprend l’épidémie d’Ebola 2018-2019 en République démocratique du Congo sur l’état de la préparation et de la riposte aux épidémies et pandémies dans le monde ? Genève : OMS (https://apps.who.int/ gpmb/assets/thematic_papers/tr-7.pdf).
- Ministère de la Santé/RDC, OMS. Rapport technique: revue après action de la riposteaux 9e, 10e, 11e et 12e Epidémie de la Maladie à virus Ebola. Cité 03 Juin2023.
- Martin I. Meltzer, Charisma Y., Scott S, Barbara K, Brett W, Estimation du nombre de cas futurs de maladie à virus Ebola pendant l’épidémie au Liberia et au Sierra Leone en 2014–2015. Centre de control et prévention des maladies. Septembre 2014/ 63(03);1-14
- D. Salem, R. Smith, A Mathematical Model of Ebola Virus Disease : Using Sensitivity Analysis to Determine Effective Intervention Targets, SCS (2016), 16–23.
☆ ESSAI DE MODÉLISATION MATHÉMATIQUE DE LA DYNAMIQUE DE TRANSMISSION DE LA MALADIE À VIRUS EBOLA DANS LA PROVINCE DU NORD-KIVU ET L’ITURI EN 2022
